Posts Tagged: clinical trial
concentric circle origami
I recently finished the second cycle of the clinical trial I’m participating in. I’ll have a bone marrow biopsy on Tuesday and about a week later the results will be the first indication of how well I’m responding to the treatment, which will probably guide future treatment. I’ve mostly tolerated it well—at times feeling crappy, and I seem to have some very slight neuropathy issues recently in my finger tips and toes, but mostly feeling pretty well. (Though lots of blood transfusions recently too.)
Besides that I’ve been working on more curved crease origami, along with trying to model it in 3D.
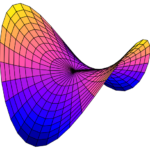
In mathematics, a developable surface is a surface that can be flattened out into a plane. Since origami starts with a flat sheet of paper, and paper doesn’t squash or stretch, the results of origami must too be a developable surface. Ruled surfaces are surfaces that can be constructed with straight lines. The hyperbolic paraboloid (also called a hypar) is a ruled surface, but not developable. The cylinder (without end caps) is both developable and ruled.
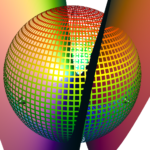
Folding concentric circles into a piece of paper seems to be both a developable surface (or at least a close approximation of one), and an approximation of a hypar. It makes me wonder if there is some kind of limit or something we could move towards, maybe as the distance between the concentric circular creases goes towards zero.
This is the second piece I’ve made with vinyl, it is very similar to the first but with the width of each concentric strip about 30% smaller. In the first one I put a sheet of aluminum foil between the two self adhesive vinyl layers, this time I tried a sheet of plastic. I’ve also been considering trying fabric and cheesecloth. I have three more sets of scored vinyl waiting to be assembled (stuck together probably with a layer of something between them) and folded. Two are variations of nested circles (not completely concentric), and one is two spirals—one forming all peaks and the other forming all troughs.
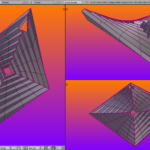
I suspect that the creases should each lie on the intersection of a hypar and a sphere. I’ve been working on making 3D models of it recently, and can tell it isn’t quite right yet, but believe it is getting close.
My next attempt will be entirely programmatically I think, inside blender with python.